Maulana Aji Faqih
34410262
1ID03
Dalam ekonomi , Cobb-Douglas bentuk fungsional dari fungsi produksi secara luas digunakan untuk mewakili hubungan output untuk input. Hal ini diusulkan oleh Knut Wicksell (1851-1926), dan diuji terhadap bukti statistik olehCharles Cobb dan Paul Douglas di 1900-1928.
Untuk produksi, fungsi ini
Y = K α β AL,
dimana:
§ Y = total produksi (nilai moneter semua barang yang diproduksi dalam setahun)
§ L = tenaga kerja input
§ K = modal input
§ α dan β adalah elastisitas output dari tenaga kerja dan modal, masing-masing. Nilai-nilai konstan ditentukan oleh teknologi yang tersedia.
Output elastisitas mengukur respons output oleh perubahan tingkat baik tenaga kerja atau modal yang digunakan dalam produksi, ceteris paribus . Sebagai contoh jika α = 0,15, peningkatan 1% tenaga kerja akan mengakibatkan kenaikan sekitar 0,15% pada output.
Selanjutnya, jika:
α + β = 1,
fungsi produksi memiliki skala hasil konstan . Artinya, jika L dan K masing-masing meningkat sebesar 20%, kenaikan Y sebesar 20%. Jika
α + β <1,
kembali ke skala yang menurun, dan jika
α + β> 1
kembali ke skala yang meningkat. Dengan asumsi persaingan sempurna dan α + β = 1, α dan β dapat ditunjukkan untuk menjadi tenaga kerja dan modal pangsa output.
Cobb dan Douglas dipengaruhi oleh bukti statistik yang muncul untuk menunjukkan bahwa tenaga kerja dan modal saham dari total output yang konstan dari waktu ke waktu di negara maju, mereka menjelaskan hal ini dengan statistik fitting -kuadrat regresi fungsi produksi mereka. Saat ini sudah ada keraguan mengenai apakah keteguhan dari waktu ke waktu ada.
Kurangnya keteguhan dari waktu ke waktu
Baik Cobb Douglas disediakan maupun teoritis alasan mengapa koefisien α dan β harus konstan dari waktu ke waktu atau sama antara sektor ekonomi. Ingat bahwa sifat mesin dan barang modal lainnya (K) berbeda antara waktu-waktu dan sesuai dengan apa yang sedang diproduksi. Begitu juga keterampilan tenaga kerja (L).
Analisis Dimensi
The-model Cobb Douglas dikritik berdasarkan analisis dimensional tidak memiliki bermakna atau ekonomis yang wajar unit pengukuran . [1] Satuan kuantitas adalah:
§ Y: widget / tahun (wid / thn)
§ L: man-hours/year (manhr / thn)
§ K: capital-hours/year (caphr / tahun; ini mengangkat isu modal heterogen)
§ α, β: nomor murni (non-dimensi), karena menjadi eksponen
§ J: (widget tahun * α + β - 1) / (α caphr * manhr β), kuantitas yang menyeimbangkan.
Model ini sesuai dikritik karena jumlah dan K L α β telah berarti unit ekonomi kecuali α = β = 1 (yang secara ekonomi tidak masuk akal, karena ada maka tidak menurun kembali ke skala ). Sebagai contoh, jika α 1 = / 2, L α memiliki satuan "akar kuadrat manusia-jam di atas akar kuadrat dari tahun", yang tidak bermakna. produktivitas faktor total A belum sulit untuk menafsirkan ekonomis.
Kurangnya microfoundations
Fungsi produksi Cobb-Douglas tidak dikembangkan atas dasar pengetahuan apapun tentang rekayasa, teknologi, atau manajemen dari proses produksi. Itu bukan dikembangkan karena memiliki karakteristik matematika yang menarik, seperti semakin berkurang marjinal ke salah satu faktor produksi dan properti bahwa pengeluaran pada setiap masukan yang diberikan adalah sebagian kecil dari total biaya konstan.
Krusial, tidak ada microfoundations untuk itu. Dalam era modern, ekonom bersikeras bahwa logika-mikro dari setiap proses skala yang lebih besar seharusnya dijelaskan. Fungsi produksi C-D gagal tes ini.
Sebagai contoh, mempertimbangkan dua sektor yang tepat Cobb-Douglas teknologi yang sama:
jika, untuk sektor 1,
Y 1 = AL 1 K 1 α β
dan, untuk sektor 2,
Y 2 = AL 2 α K 2 β,
bahwa, secara umum, tidak berarti bahwa
Y 1 + Y 2 = A (L 1 + L 2) α (K 1 + K 2) β
Hal ini berlaku hanya jika L 1 / L 2 = K 1 / K 2 dan α + β = 1, yaitu bagi hasil yang konstan untuk teknologi skala.
Dengan demikian kesalahan matematika untuk berasumsi bahwa hanya karena fungsi Cobb-Douglas berlaku di tingkat mikro, hal itu juga berlaku pada tingkat makro. Demikian pula, tidak ada alasan bahwa makro Cobb-Douglas berlaku di tingkat dipisahkan.
Sebuah microfoundation teknologi Cobb-Douglas agregat berdasarkan kegiatan linear diperoleh di: Distribusi Pareto dan Cobb-Douglas Fungsi Produksi dalam Aktivitas Analisis, HS Houthakker, Kajian Studi Ekonomi, Vol. 23, No 1 (1955-1956), hlm 27-31.
Meskipun demikian, fungsi Cobb-Douglas telah diterapkan pada banyak konteks lain selain produksi. Hal ini dapat diterapkan untuk utilitas sebagai berikut: U (x 1, x 2) = x 1 x 2 α β;dimana x 1 dan x 2 adalah jumlah yang dikonsumsi yang baik # 1 dan baik # 2.
Dalam bentuk umum, di mana x 1, x 2, ... , X L adalah jumlah yang dikonsumsi yang baik # 1, baik # 2, ..., bagus # L, sebuah fungsi utilitas yang mewakili preferensi Cobb-Douglas dapat ditulis sebagai:

dengan x = (x 1, x 2, ..., x L). Setting λ = λ 1 + λ 2 + ... + Λ L dan karena fungsi

adalah sangat monoton untuk x> 0, berarti

mewakili preferensi yang sama. Mengatur i α = λ i / λ dapat ditunjukkan bahwa
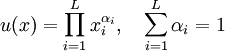
utilitas ini dapat dimaksimalkan dengan melihat logaritma dari utilitas

dan masalahnya adalah

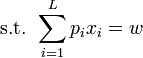
The fungsi Lagrange adalah

Kondisi urutan pertama adalah

dan sejak
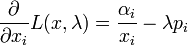
kondisi hasil

Membagi ekspresi untuk i dengan ekspresi untuk j membatalkan λ dan menghasilkan

dan selanjutnya

Menjumlahkan i memberi kita

Mengingat bahwa jumlah i α 1 dan kendala yang kita miliki
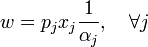
dan akhirnya
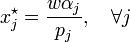
Sumber : WIKIPEDIA.COM
Tidak ada komentar:
Posting Komentar